Note
Go to the end to download the full example code
Using Custom Kernels within TensorRT Engines with Torch-TensorRT¶
We are going to demonstrate how a developer could include a custom kernel in a TensorRT engine using Torch-TensorRT
Torch-TensorRT supports falling back to PyTorch implementations of operations in the case that Torch-TensorRT does not know how to compile them in TensorRT. However, this comes at the cost of a graph break and will reduce the performance of the model. The easiest way to fix lack of support for ops is by adding a decomposition (see: Writing lowering passes for the Dynamo frontend) - which defines the operator in terms of PyTorch ops that are supported in Torch-TensorRT or a converter (see: Writing converters for the Dynamo frontend) - which defines the operator in terms of TensorRT operators.
In some cases there isn’t a great way to do either of these, perhaps because the operator is a custom kernel that is not part of standard PyTorch or TensorRT cannot support it natively.
For these cases, it is possible to use a TensorRT plugin to replace the operator inside the TensorRT engine, thereby avoiding the performance and resource overhead from a graph break. For the sake of demonstration, consider the operation circular padding. Circular padding is useful for ops like circular convolution in deep learning. The following image denotes how the original image (red) is circular padded once (green) and twice (blue):
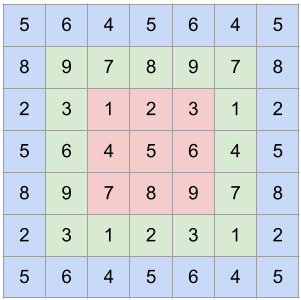
Writing Custom Operators in PyTorch¶
Assume for whatever reason we would like to use a custom implementation of circular padding. In this case as implemented using a kernel written in OpenAI Triton
When using custom kernels with PyTorch, it is recommended to take the additional step of registering them as formal operators in PyTorch. This will both make it easier to handle the operation in Torch-TensorRT and simplify its use in PyTorch. This could either be done as part of a C++ library or in Python. (see: Custom ops in C++ and Python custom ops for more details )
from typing import Any, Sequence
import numpy as np
import torch
import triton
import triton.language as tl
from torch.library import custom_op
# Defining the kernel to be run on the GPU
@triton.jit # type: ignore
def circ_pad_kernel(
X: torch.Tensor,
all_pads_0: tl.int32,
all_pads_2: tl.int32,
all_pads_4: tl.int32,
all_pads_6: tl.int32,
orig_dims_0: tl.int32,
orig_dims_1: tl.int32,
orig_dims_2: tl.int32,
orig_dims_3: tl.int32,
Y: torch.Tensor,
Y_shape_1: tl.int32,
Y_shape_2: tl.int32,
Y_shape_3: tl.int32,
X_len: tl.int32,
Y_len: tl.int32,
BLOCK_SIZE: tl.constexpr,
) -> None:
pid = tl.program_id(0)
i = pid * BLOCK_SIZE + tl.arange(0, BLOCK_SIZE)
mask_y = i < Y_len
i3 = i % Y_shape_3
i2 = (i // Y_shape_3) % Y_shape_2
i1 = (i // Y_shape_3 // Y_shape_2) % Y_shape_1
i0 = i // Y_shape_3 // Y_shape_2 // Y_shape_1
j0 = (i0 - all_pads_0 + orig_dims_0) % orig_dims_0
j1 = (i1 - all_pads_2 + orig_dims_1) % orig_dims_1
j2 = (i2 - all_pads_4 + orig_dims_2) % orig_dims_2
j3 = (i3 - all_pads_6 + orig_dims_3) % orig_dims_3
load_idx = (
orig_dims_3 * orig_dims_2 * orig_dims_1 * j0
+ orig_dims_3 * orig_dims_2 * j1
+ orig_dims_3 * j2
+ j3
)
mask_x = load_idx < X_len
x = tl.load(X + load_idx, mask=mask_x)
tl.store(Y + i, x, mask=mask_y)
# The launch code wrapped to expose it as a custom operator in our namespace
@custom_op("torchtrt_ex::triton_circular_pad", mutates_args=()) # type: ignore[misc]
def triton_circular_pad(x: torch.Tensor, padding: Sequence[int]) -> torch.Tensor:
out_dims = np.ones(len(x.shape), dtype=np.int32)
for i in range(np.size(padding) // 2):
out_dims[len(out_dims) - i - 1] = (
x.shape[len(out_dims) - i - 1] + padding[i * 2] + padding[i * 2 + 1]
)
y = torch.empty(tuple(out_dims.tolist()), device=x.device)
N = len(x.shape)
all_pads = np.zeros((N * 2,), dtype=np.int32)
orig_dims = np.array(x.shape, dtype=np.int32)
out_dims = np.array(x.shape, dtype=np.int32)
for i in range(len(padding) // 2):
out_dims[N - i - 1] += padding[i * 2] + padding[i * 2 + 1]
all_pads[N * 2 - 2 * i - 2] = padding[i * 2]
all_pads[N * 2 - 2 * i - 1] = padding[i * 2 + 1]
blockSize = 256
numBlocks = (int((np.prod(out_dims) + blockSize - 1) // blockSize),)
circ_pad_kernel[numBlocks](
x,
all_pads[0],
all_pads[2],
all_pads[4],
all_pads[6],
orig_dims[0],
orig_dims[1],
orig_dims[2],
orig_dims[3],
y,
out_dims[1],
out_dims[2],
out_dims[3],
int(np.prod(orig_dims)),
int(np.prod(out_dims)),
BLOCK_SIZE=256,
)
return y
Above is all that is required to create a custom operator for PyTorch. We can now call it directly as torch.ops.torchtrt_ex.triton_circular_pad
Testing our custom op¶
The native PyTorch implementation
ex_input = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3).to("cuda")
padding = (1, 1, 2, 0)
torch.nn.functional.pad(ex_input, padding, "circular")
tensor([[[[5., 3., 4., 5., 3.],
[8., 6., 7., 8., 6.],
[2., 0., 1., 2., 0.],
[5., 3., 4., 5., 3.],
[8., 6., 7., 8., 6.]]]], device='cuda:0')
Our custom implementation
torch.ops.torchtrt_ex.triton_circular_pad(ex_input, padding)
tensor([[[[5., 3., 4., 5., 3.],
[8., 6., 7., 8., 6.],
[2., 0., 1., 2., 0.],
[5., 3., 4., 5., 3.],
[8., 6., 7., 8., 6.]]]], device='cuda:0')
We have defined the minimum to start using our custom op in PyTorch, but to take the extra step of making this operator tracable by Dynamo (a prerequisite for being supported in Torch-TensorRT), we need to define a “Fake Tensor” implementation of the op. This function defines the effect that our kernel would have on input tensors in terms of native PyTorch ops. It allows Dynamo to calculate tensor properties like sizes, stride, device etc. without needing to use real data (More information here). In our case we can just use the native circular pad operation as our FakeTensor implementation.
@torch.library.register_fake("torchtrt_ex::triton_circular_pad") # type: ignore[misc]
def _(x: torch.Tensor, padding: Sequence[int]) -> torch.Tensor:
return torch.nn.functional.pad(x, padding, "circular")
# Additionally one may want to define an autograd implementation for the backwards pass to round out the custom op implementation but that is beyond the scope of this tutorial (see https://pytorch.org/docs/main/library.html#torch.library.register_autograd for more)
Using the Custom Operator in a Model¶
We can now create models using our custom op. Here is a small example one that uses both natively supported operators (Convolution) and our custom op.
from typing import Sequence
from torch import nn
class MyModel(nn.Module): # type: ignore[misc]
def __init__(self, padding: Sequence[int]):
super().__init__()
self.padding = padding
self.conv = nn.Conv2d(1, 5, kernel_size=3)
def forward(self, x: torch.Tensor) -> torch.Tensor:
padded_x = torch.ops.torchtrt_ex.triton_circular_pad(x, self.padding)
y = self.conv(padded_x)
return y
my_model = MyModel((1, 1, 2, 0)).to("cuda")
my_model(ex_input)
tensor([[[[-0.2604, -0.4232, -0.3041],
[-3.0833, -3.2461, -3.1270],
[-0.2450, -0.4079, -0.2887]],
[[ 0.2828, -0.0373, 1.0332],
[-2.3143, -2.6344, -1.5638],
[-1.1867, -1.5068, -0.4363]],
[[ 1.7937, 1.3488, 2.1350],
[ 0.7966, 0.3517, 1.1379],
[ 3.5537, 3.1088, 3.8950]],
[[-1.0550, -0.6163, -1.0109],
[ 0.5245, 0.9632, 0.5686],
[ 0.3775, 0.8162, 0.4216]],
[[-0.4311, -0.1649, -1.2091],
[-4.3668, -4.1006, -5.1447],
[-5.0352, -4.7689, -5.8131]]]], device='cuda:0')
If we try to compile this model with Torch-TensorRT, we can see that (as of Torch-TensorRT 2.4.0) a number of subgraphs are created to run the custom op in PyTorch and the convolution in TensorRT
import torch_tensorrt as torchtrt
torchtrt.compile(
my_model,
inputs=[ex_input],
dryrun=True, # Check the support of the model without having to build the engines
min_block_size=1,
)
GraphModule(
(_run_on_gpu_0): GraphModule()
(_run_on_acc_1): GraphModule(
(conv): Module()
)
)
++++++++++++++ Dry-Run Results for Graph +++++++++++++++++
The graph consists of 2 Total Operators, of which 1 operators are supported, 50.0% coverage
The following ops are currently unsupported or excluded from conversion, and are listed with their op-count in the graph:
torch.ops.torchtrt_ex.triton_circular_pad.default: 1
The following nodes are currently set to run in Torch:
Node: torch.ops.torchtrt_ex.triton_circular_pad.default, with layer location: __/triton_circular_pad
Note: Some of the above nodes may be supported, but were not included in a TRT graph by the partitioner
Compiled with: CompilationSettings(enabled_precisions={<dtype.f32: 7>}, debug=False, workspace_size=0, min_block_size=1, torch_executed_ops=set(), pass_through_build_failures=False, max_aux_streams=None, version_compatible=False, optimization_level=None, use_python_runtime=False, truncate_double=False, use_fast_partitioner=True, enable_experimental_decompositions=False, device=Device(type=DeviceType.GPU, gpu_id=0), require_full_compilation=False, disable_tf32=False, sparse_weights=False, refit=False, engine_capability=<EngineCapability.STANDARD: 1>, num_avg_timing_iters=1, dla_sram_size=1048576, dla_local_dram_size=1073741824, dla_global_dram_size=536870912, dryrun=True, hardware_compatible=False)
Graph Structure:
Inputs: List[Tensor: (1, 1, 3, 3)@float32]
...
TRT Engine #1 - Submodule name: _run_on_acc_1
Engine Inputs: List[Tensor: (1, 1, 5, 5)@float32]
Number of Operators in Engine: 1
Engine Outputs: Tensor: (1, 5, 3, 3)@float32
...
Outputs: List[Tensor: (1, 5, 3, 3)@float32]
--------- Aggregate Stats ---------
Average Number of Operators per TRT Engine: 1.0
Most Operators in a TRT Engine: 1
********** Recommendations **********
- For minimal graph segmentation, select min_block_size=1 which would generate 1 TRT engine(s)
- The current level of graph segmentation is equivalent to selecting min_block_size=1 which generates 1 TRT engine(s)
We see that there is going to be 2 subgraphs, one that will run through PyTorch for our custom op and one through TensorRT for the convolution. This graph break is going to be a significant portion of the latency of this model.
Wrapping Custom Kernels to use in TensorRT¶
To address this graph break, the first step is to make our kernel implementation available in TensorRT. Again this can be done in either C++ or Python. For the actual details on how to implement TensorRT plugins refer here. From a high level, similar to PyTorch you will need to define systems to handle setting up the operator, calculating the effect of the operation abstractly, serializing the op and the actual mechanics of calling the implementation of the op in the engine.
import pickle as pkl
from typing import Any, List, Optional, Self
import cupy as cp # Needed to work around API gaps in PyTorch to build torch.Tensors around preallocated CUDA memory
import numpy as np
import tensorrt as trt
class CircularPaddingPlugin(trt.IPluginV2DynamicExt): # type: ignore[misc]
def __init__(
self, field_collection: Optional[List[trt.PluginFieldCollection]] = None
):
super().__init__()
self.pads = []
self.X_shape: List[int] = []
self.num_outputs = 1
self.plugin_namespace = ""
self.plugin_type = "CircularPaddingPlugin"
self.plugin_version = "1"
if field_collection is not None:
assert field_collection[0].name == "pads"
self.pads = field_collection[0].data
def get_output_datatype(
self, index: int, input_types: List[trt.DataType]
) -> trt.DataType:
return input_types[0]
def get_output_dimensions(
self,
output_index: int,
inputs: List[trt.DimsExprs],
exprBuilder: trt.IExprBuilder,
) -> trt.DimsExprs:
output_dims = trt.DimsExprs(inputs[0])
for i in range(np.size(self.pads) // 2):
output_dims[len(output_dims) - i - 1] = exprBuilder.operation(
trt.DimensionOperation.SUM,
inputs[0][len(output_dims) - i - 1],
exprBuilder.constant(self.pads[i * 2] + self.pads[i * 2 + 1]),
)
return output_dims
def configure_plugin(
self,
inp: List[trt.DynamicPluginTensorDesc],
out: List[trt.DynamicPluginTensorDesc],
) -> None:
X_dims = inp[0].desc.dims
self.X_shape = np.zeros((len(X_dims),))
for i in range(len(X_dims)):
self.X_shape[i] = X_dims[i]
def serialize(self) -> bytes:
return pkl.dumps({"pads": self.pads})
def supports_format_combination(
self, pos: int, in_out: List[trt.PluginTensorDesc], num_inputs: int
) -> bool:
assert num_inputs == 1
assert pos < len(in_out)
desc = in_out[pos]
if desc.format != trt.TensorFormat.LINEAR:
return False
# first input should be float16 or float32
if pos == 0:
return bool(
(desc.type == trt.DataType.FLOAT) or desc.type == (trt.DataType.HALF)
)
# output should have the same type as the input
if pos == 1:
return bool((in_out[0].type == desc.type))
return False
def enqueue(
self,
input_desc: List[trt.PluginTensorDesc],
output_desc: List[trt.PluginTensorDesc],
inputs: List[int],
outputs: List[int],
workspace: int,
stream: int,
) -> None:
# Host code is slightly different as this will be run as part of the TRT execution
in_dtype = torchtrt.dtype.try_from(input_desc[0].type).to(np.dtype)
a_mem = cp.cuda.UnownedMemory(
inputs[0], np.prod(input_desc[0].dims) * cp.dtype(in_dtype).itemsize, self
)
c_mem = cp.cuda.UnownedMemory(
outputs[0],
np.prod(output_desc[0].dims) * cp.dtype(in_dtype).itemsize,
self,
)
a_ptr = cp.cuda.MemoryPointer(a_mem, 0)
c_ptr = cp.cuda.MemoryPointer(c_mem, 0)
a_d = cp.ndarray((np.prod(input_desc[0].dims)), dtype=in_dtype, memptr=a_ptr)
c_d = cp.ndarray((np.prod(output_desc[0].dims)), dtype=in_dtype, memptr=c_ptr)
a_t = torch.as_tensor(a_d, device="cuda")
c_t = torch.as_tensor(c_d, device="cuda")
N = len(self.X_shape)
all_pads = np.zeros((N * 2,), dtype=np.int32)
orig_dims = np.array(self.X_shape, dtype=np.int32)
out_dims = np.array(self.X_shape, dtype=np.int32)
for i in range(np.size(self.pads) // 2):
out_dims[N - i - 1] += self.pads[i * 2] + self.pads[i * 2 + 1]
all_pads[N * 2 - 2 * i - 2] = self.pads[i * 2]
all_pads[N * 2 - 2 * i - 1] = self.pads[i * 2 + 1]
all_pads = all_pads.tolist()
orig_dims = orig_dims.tolist()
out_dims = out_dims.tolist()
blockSize = 256
numBlocks = (int((np.prod(out_dims) + blockSize - 1) // blockSize),)
# Call the same kernel implementation we use in PyTorch
circ_pad_kernel[numBlocks](
a_t,
all_pads[0],
all_pads[2],
all_pads[4],
all_pads[6],
orig_dims[0],
orig_dims[1],
orig_dims[2],
orig_dims[3],
c_t,
out_dims[1],
out_dims[2],
out_dims[3],
int(np.prod(orig_dims)),
int(np.prod(out_dims)),
BLOCK_SIZE=256,
)
def clone(self) -> Self:
cloned_plugin = CircularPaddingPlugin()
cloned_plugin.__dict__.update(self.__dict__)
return cloned_plugin
class CircularPaddingPluginCreator(trt.IPluginCreator): # type: ignore[misc]
def __init__(self):
super().__init__()
self.name = "CircularPaddingPlugin"
self.plugin_namespace = ""
self.plugin_version = "1"
self.field_names = trt.PluginFieldCollection(
[trt.PluginField("pads", np.array([]), trt.PluginFieldType.INT32)]
)
def create_plugin(
self, name: str, field_collection: trt.PluginFieldCollection_
) -> CircularPaddingPlugin:
return CircularPaddingPlugin(field_collection)
def deserialize_plugin(self, name: str, data: bytes) -> CircularPaddingPlugin:
pads_dict = pkl.loads(data)
print(pads_dict)
deserialized = CircularPaddingPlugin()
deserialized.__dict__.update(pads_dict)
print(deserialized.pads)
return deserialized
# Register the plugin creator in the TensorRT Plugin Registry
TRT_PLUGIN_REGISTRY = trt.get_plugin_registry()
TRT_PLUGIN_REGISTRY.register_creator(CircularPaddingPluginCreator(), "") # type: ignore[no-untyped-call]
Using Torch-TensorRT to Insert the Kernel¶
Now with our TensorRT plugin, we can create a converter so that Torch-TensorRT knows to insert our plugin in place of our custom circular padding operator. More information on writing converters can be found here
from typing import Dict, Tuple
from torch.fx.node import Argument, Target
from torch_tensorrt.dynamo.conversion import (
ConversionContext,
dynamo_tensorrt_converter,
)
from torch_tensorrt.dynamo.conversion.converter_utils import get_trt_tensor
from torch_tensorrt.fx.converters.converter_utils import set_layer_name
@dynamo_tensorrt_converter(
torch.ops.torchtrt_ex.triton_circular_pad.default
) # type: ignore
# Recall the schema defined above:
# torch.ops.torchtrt_ex.triton_circular_pad.default(Tensor x, IntList padding) -> Tensor
def circular_padding_converter(
ctx: ConversionContext,
target: Target,
args: Tuple[Argument, ...],
kwargs: Dict[str, Argument],
name: str,
):
# How to retrieve a plugin if it is defined elsewhere (e.g. linked library)
plugin_registry = trt.get_plugin_registry()
plugin_creator = plugin_registry.get_plugin_creator(
type="CircularPaddingPlugin", version="1", plugin_namespace=""
)
assert plugin_creator, f"Unable to find CircularPaddingPlugin creator"
# Pass configurations to the plugin implementation
field_configs = trt.PluginFieldCollection(
[
trt.PluginField(
"pads",
np.array(
args[1], dtype=np.int32
), # Arg 1 of `torch.ops.torchtrt_ex.triton_circular_pad` is the int list containing the padding settings. Note: the dtype matters as you are eventually passing this as a c-like buffer
trt.PluginFieldType.INT32,
),
]
)
plugin = plugin_creator.create_plugin(name=name, field_collection=field_configs)
assert plugin, "Unable to create CircularPaddingPlugin"
input_tensor = args[
0
] # Arg 0 `torch.ops.torchtrt_ex.triton_circular_pad` is the input tensor
if not isinstance(input_tensor, trt.ITensor):
# Freeze input tensor if not TensorRT Tensor already
input_tensor = get_trt_tensor(ctx, input_tensor, f"{name}_input")
layer = ctx.net.add_plugin_v2(
[input_tensor], plugin
) # Add the plugin to the network being constructed
layer.name = f"circular_padding_plugin-{name}"
return layer.get_output(0)
Finally, we are now able to fully compile our model
trt_model = torchtrt.compile(
my_model,
inputs=[ex_input],
min_block_size=1,
)
GraphModule(
(_run_on_acc_0): TorchTensorRTModule()
)
+++++++++++++++ Dry-Run Results for Graph ++++++++++++++++
The graph consists of 2 Total Operators, of which 2 operators are supported, 100.0% coverage
Compiled with: CompilationSettings(enabled_precisions={<dtype.f32: 7>}, debug=True, workspace_size=0, min_block_size=1, torch_executed_ops=set(), pass_through_build_failures=False, max_aux_streams=None, version_compatible=False, optimization_level=None, use_python_runtime=False, truncate_double=False, use_fast_partitioner=True, enable_experimental_decompositions=False, device=Device(type=DeviceType.GPU, gpu_id=0), require_full_compilation=False, disable_tf32=False, sparse_weights=False, refit=False, engine_capability=<EngineCapability.STANDARD: 1>, num_avg_timing_iters=1, dla_sram_size=1048576, dla_local_dram_size=1073741824, dla_global_dram_size=536870912, dryrun=False, hardware_compatible=False)
Graph Structure:
Inputs: List[Tensor: (1, 1, 3, 3)@float32]
...
TRT Engine #1 - Submodule name: _run_on_acc_0
Engine Inputs: List[Tensor: (1, 1, 3, 3)@float32]
Number of Operators in Engine: 2
Engine Outputs: Tensor: (1, 5, 3, 3)@float32
...
Outputs: List[Tensor: (1, 5, 3, 3)@float32]
---------- Aggregate Stats -------------
Average Number of Operators per TRT Engine: 2.0
Most Operators in a TRT Engine: 2
********** Recommendations **********
- For minimal graph segmentation, select min_block_size=2 which would generate 1 TRT engine(s)
- The current level of graph segmentation is equivalent to selecting min_block_size=2 which generates 1 TRT engine(s)
As you can see, now there is only one subgraph created for the TensorRT engine that contains both our custom kernel and the native convolution operator.
print(trt_model(ex_input))
tensor([[[[-0.2604, -0.4232, -0.3041],
[-3.0833, -3.2461, -3.1270],
[-0.2450, -0.4079, -0.2887]],
[[ 0.2828, -0.0373, 1.0332],
[-2.3143, -2.6344, -1.5638],
[-1.1867, -1.5068, -0.4363]],
[[ 1.7937, 1.3488, 2.1350],
[ 0.7966, 0.3517, 1.1379],
[ 3.5537, 3.1088, 3.8950]],
[[-1.0550, -0.6163, -1.0109],
[ 0.5245, 0.9632, 0.5686],
[ 0.3775, 0.8162, 0.4216]],
[[-0.4311, -0.1649, -1.2091],
[-4.3668, -4.1006, -5.1447],
[-5.0352, -4.7689, -5.8131]]]], device='cuda:0')
We can verify our implementation is run correctly by both TensorRT and PyTorch
print(my_model(ex_input) - trt_model(ex_input))
tensor([[[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]]]], device='cuda:0', grad_fn=<SubBackward0>)
Total running time of the script: ( 0 minutes 0.000 seconds)
