Spatial Transformer Networks Tutorial

Author: Ghassen HAMROUNI

In this tutorial, you will learn how to augment your network using a visual attention mechanism called spatial transformer networks. You can read more about the spatial transformer networks in the DeepMind paper

Spatial transformer networks are a generalization of differentiable attention to any spatial transformation. Spatial transformer networks (STN for short) allow a neural network to learn how to perform spatial transformations on the input image in order to enhance the geometric invariance of the model. For example, it can crop a region of interest, scale and correct the orientation of an image. It can be a useful mechanism because CNNs are not invariant to rotation and scale and more general affine transformations.

One of the best things about STN is the ability to simply plug it into any existing CNN with very little modification.

# License: BSD
# Author: Ghassen Hamrouni

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy as np

plt.ion()   # interactive mode

<contextlib.ExitStack object at 0x7f4da6487880>

Loading the data

In this post we experiment with the classic MNIST dataset. Using a standard convolutional network augmented with a spatial transformer network.

from six.moves import urllib
opener = urllib.request.build_opener()
opener.addheaders = [('User-agent', 'Mozilla/5.0')]
urllib.request.install_opener(opener)

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Training dataset
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST(root='.', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])), batch_size=64, shuffle=True, num_workers=4)
# Test dataset
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST(root='.', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])), batch_size=64, shuffle=True, num_workers=4)

Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Failed to download (trying next):
HTTP Error 403: Forbidden

Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-images-idx3-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-images-idx3-ubyte.gz to ./MNIST/raw/train-images-idx3-ubyte.gz

  0%|          | 0/9912422 [00:00<?, ?it/s]
100%|##########| 9912422/9912422 [00:00<00:00, 129066611.34it/s]
Extracting ./MNIST/raw/train-images-idx3-ubyte.gz to ./MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Failed to download (trying next):
HTTP Error 403: Forbidden

Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-labels-idx1-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-labels-idx1-ubyte.gz to ./MNIST/raw/train-labels-idx1-ubyte.gz

  0%|          | 0/28881 [00:00<?, ?it/s]
100%|##########| 28881/28881 [00:00<00:00, 14810575.11it/s]
Extracting ./MNIST/raw/train-labels-idx1-ubyte.gz to ./MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Failed to download (trying next):
HTTP Error 403: Forbidden

Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-images-idx3-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-images-idx3-ubyte.gz to ./MNIST/raw/t10k-images-idx3-ubyte.gz

  0%|          | 0/1648877 [00:00<?, ?it/s]
100%|##########| 1648877/1648877 [00:00<00:00, 159864344.25it/s]
Extracting ./MNIST/raw/t10k-images-idx3-ubyte.gz to ./MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Failed to download (trying next):
HTTP Error 403: Forbidden

Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-labels-idx1-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-labels-idx1-ubyte.gz to ./MNIST/raw/t10k-labels-idx1-ubyte.gz

  0%|          | 0/4542 [00:00<?, ?it/s]
100%|##########| 4542/4542 [00:00<00:00, 2705656.69it/s]
Extracting ./MNIST/raw/t10k-labels-idx1-ubyte.gz to ./MNIST/raw

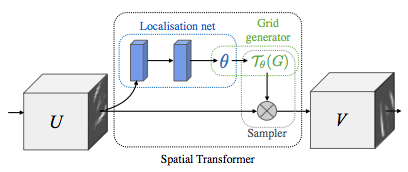
Depicting spatial transformer networks

Spatial transformer networks boils down to three main components :

• The localization network is a regular CNN which regresses the transformation parameters. The transformation is never learned explicitly from this dataset, instead the network learns automatically the spatial transformations that enhances the global accuracy.

• The grid generator generates a grid of coordinates in the input image corresponding to each pixel from the output image.

• The sampler uses the parameters of the transformation and applies it to the input image.

Note

We need the latest version of PyTorch that contains affine_grid and grid_sample modules.

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)

        # Spatial transformer localization-network
        self.localization = nn.Sequential(
            nn.Conv2d(1, 8, kernel_size=7),
            nn.MaxPool2d(2, stride=2),
            nn.ReLU(True),
            nn.Conv2d(8, 10, kernel_size=5),
            nn.MaxPool2d(2, stride=2),
            nn.ReLU(True)
        )

        # Regressor for the 3 * 2 affine matrix
        self.fc_loc = nn.Sequential(
            nn.Linear(10 * 3 * 3, 32),
            nn.ReLU(True),
            nn.Linear(32, 3 * 2)
        )

        # Initialize the weights/bias with identity transformation
        self.fc_loc[2].weight.data.zero_()
        self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))

    # Spatial transformer network forward function
    def stn(self, x):
        xs = self.localization(x)
        xs = xs.view(-1, 10 * 3 * 3)
        theta = self.fc_loc(xs)
        theta = theta.view(-1, 2, 3)

        grid = F.affine_grid(theta, x.size())
        x = F.grid_sample(x, grid)

        return x

    def forward(self, x):
        # transform the input
        x = self.stn(x)

        # Perform the usual forward pass
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)


model = Net().to(device)

Training the model

Now, let’s use the SGD algorithm to train the model. The network is learning the classification task in a supervised way. In the same time the model is learning STN automatically in an end-to-end fashion.

optimizer = optim.SGD(model.parameters(), lr=0.01)


def train(epoch):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)

        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % 500 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))
#
# A simple test procedure to measure the STN performances on MNIST.
#


def test():
    with torch.no_grad():
        model.eval()
        test_loss = 0
        correct = 0
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)

            # sum up batch loss
            test_loss += F.nll_loss(output, target, size_average=False).item()
            # get the index of the max log-probability
            pred = output.max(1, keepdim=True)[1]
            correct += pred.eq(target.view_as(pred)).sum().item()

        test_loss /= len(test_loader.dataset)
        print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'
              .format(test_loss, correct, len(test_loader.dataset),
                      100. * correct / len(test_loader.dataset)))

Visualizing the STN results

Now, we will inspect the results of our learned visual attention mechanism.

We define a small helper function in order to visualize the transformations while training.

def convert_image_np(inp):
    """Convert a Tensor to numpy image."""
    inp = inp.numpy().transpose((1, 2, 0))
    mean = np.array([0.485, 0.456, 0.406])
    std = np.array([0.229, 0.224, 0.225])
    inp = std * inp + mean
    inp = np.clip(inp, 0, 1)
    return inp

# We want to visualize the output of the spatial transformers layer
# after the training, we visualize a batch of input images and
# the corresponding transformed batch using STN.


def visualize_stn():
    with torch.no_grad():
        # Get a batch of training data
        data = next(iter(test_loader))[0].to(device)

        input_tensor = data.cpu()
        transformed_input_tensor = model.stn(data).cpu()

        in_grid = convert_image_np(
            torchvision.utils.make_grid(input_tensor))

        out_grid = convert_image_np(
            torchvision.utils.make_grid(transformed_input_tensor))

        # Plot the results side-by-side
        f, axarr = plt.subplots(1, 2)
        axarr[0].imshow(in_grid)
        axarr[0].set_title('Dataset Images')

        axarr[1].imshow(out_grid)
        axarr[1].set_title('Transformed Images')

for epoch in range(1, 20 + 1):
    train(epoch)
    test()

# Visualize the STN transformation on some input batch
visualize_stn()

plt.ioff()
plt.show()

Train Epoch: 1 [0/60000 (0%)]   Loss: 2.315648
Train Epoch: 1 [32000/60000 (53%)]      Loss: 1.088514

Test set: Average loss: 0.2533, Accuracy: 9297/10000 (93%)

Train Epoch: 2 [0/60000 (0%)]   Loss: 0.554237
Train Epoch: 2 [32000/60000 (53%)]      Loss: 0.345812

Test set: Average loss: 0.1460, Accuracy: 9587/10000 (96%)

Train Epoch: 3 [0/60000 (0%)]   Loss: 0.340843
Train Epoch: 3 [32000/60000 (53%)]      Loss: 0.244480

Test set: Average loss: 0.1058, Accuracy: 9684/10000 (97%)

Train Epoch: 4 [0/60000 (0%)]   Loss: 0.381258
Train Epoch: 4 [32000/60000 (53%)]      Loss: 0.215038

Test set: Average loss: 0.1120, Accuracy: 9669/10000 (97%)

Train Epoch: 5 [0/60000 (0%)]   Loss: 0.177647
Train Epoch: 5 [32000/60000 (53%)]      Loss: 0.166256

Test set: Average loss: 0.0951, Accuracy: 9718/10000 (97%)

Train Epoch: 6 [0/60000 (0%)]   Loss: 0.133605
Train Epoch: 6 [32000/60000 (53%)]      Loss: 0.091024

Test set: Average loss: 0.0740, Accuracy: 9778/10000 (98%)

Train Epoch: 7 [0/60000 (0%)]   Loss: 0.055931
Train Epoch: 7 [32000/60000 (53%)]      Loss: 0.171603

Test set: Average loss: 0.1799, Accuracy: 9436/10000 (94%)

Train Epoch: 8 [0/60000 (0%)]   Loss: 0.572894
Train Epoch: 8 [32000/60000 (53%)]      Loss: 0.088160

Test set: Average loss: 0.0690, Accuracy: 9801/10000 (98%)

Train Epoch: 9 [0/60000 (0%)]   Loss: 0.092760
Train Epoch: 9 [32000/60000 (53%)]      Loss: 0.107107

Test set: Average loss: 0.0630, Accuracy: 9816/10000 (98%)

Train Epoch: 10 [0/60000 (0%)]  Loss: 0.094078
Train Epoch: 10 [32000/60000 (53%)]     Loss: 0.198737

Test set: Average loss: 0.0547, Accuracy: 9829/10000 (98%)

Train Epoch: 11 [0/60000 (0%)]  Loss: 0.139445
Train Epoch: 11 [32000/60000 (53%)]     Loss: 0.085205

Test set: Average loss: 0.0629, Accuracy: 9809/10000 (98%)

Train Epoch: 12 [0/60000 (0%)]  Loss: 0.070778
Train Epoch: 12 [32000/60000 (53%)]     Loss: 0.142280

Test set: Average loss: 0.0533, Accuracy: 9838/10000 (98%)

Train Epoch: 13 [0/60000 (0%)]  Loss: 0.096739
Train Epoch: 13 [32000/60000 (53%)]     Loss: 0.124326

Test set: Average loss: 0.0542, Accuracy: 9838/10000 (98%)

Train Epoch: 14 [0/60000 (0%)]  Loss: 0.060196
Train Epoch: 14 [32000/60000 (53%)]     Loss: 0.202736

Test set: Average loss: 0.0595, Accuracy: 9836/10000 (98%)

Train Epoch: 15 [0/60000 (0%)]  Loss: 0.023419
Train Epoch: 15 [32000/60000 (53%)]     Loss: 0.134728

Test set: Average loss: 0.0478, Accuracy: 9867/10000 (99%)

Train Epoch: 16 [0/60000 (0%)]  Loss: 0.059846
Train Epoch: 16 [32000/60000 (53%)]     Loss: 0.268629

Test set: Average loss: 0.0453, Accuracy: 9870/10000 (99%)

Train Epoch: 17 [0/60000 (0%)]  Loss: 0.254969
Train Epoch: 17 [32000/60000 (53%)]     Loss: 0.313065

Test set: Average loss: 0.0536, Accuracy: 9848/10000 (98%)

Train Epoch: 18 [0/60000 (0%)]  Loss: 0.037190
Train Epoch: 18 [32000/60000 (53%)]     Loss: 0.108911

Test set: Average loss: 0.0464, Accuracy: 9867/10000 (99%)

Train Epoch: 19 [0/60000 (0%)]  Loss: 0.050956
Train Epoch: 19 [32000/60000 (53%)]     Loss: 0.096646

Test set: Average loss: 0.0427, Accuracy: 9871/10000 (99%)

Train Epoch: 20 [0/60000 (0%)]  Loss: 0.055401
Train Epoch: 20 [32000/60000 (53%)]     Loss: 0.099763

Test set: Average loss: 0.0841, Accuracy: 9769/10000 (98%)